my balanced train unloader

Smart setups of railway stations, intelligent routing, solutions to complex train-routing problems.
Please provide - only if it makes sense of course - a blueprint of your creation.
Post Reply
Copy link
massa84
Manual Inserter
Manual Inserter
Posts: 3
Joined: Wed Dec 13, 2017 11:10 pm
Contact:
Contact massa84

my balanced train unloader

Post by massa84 »


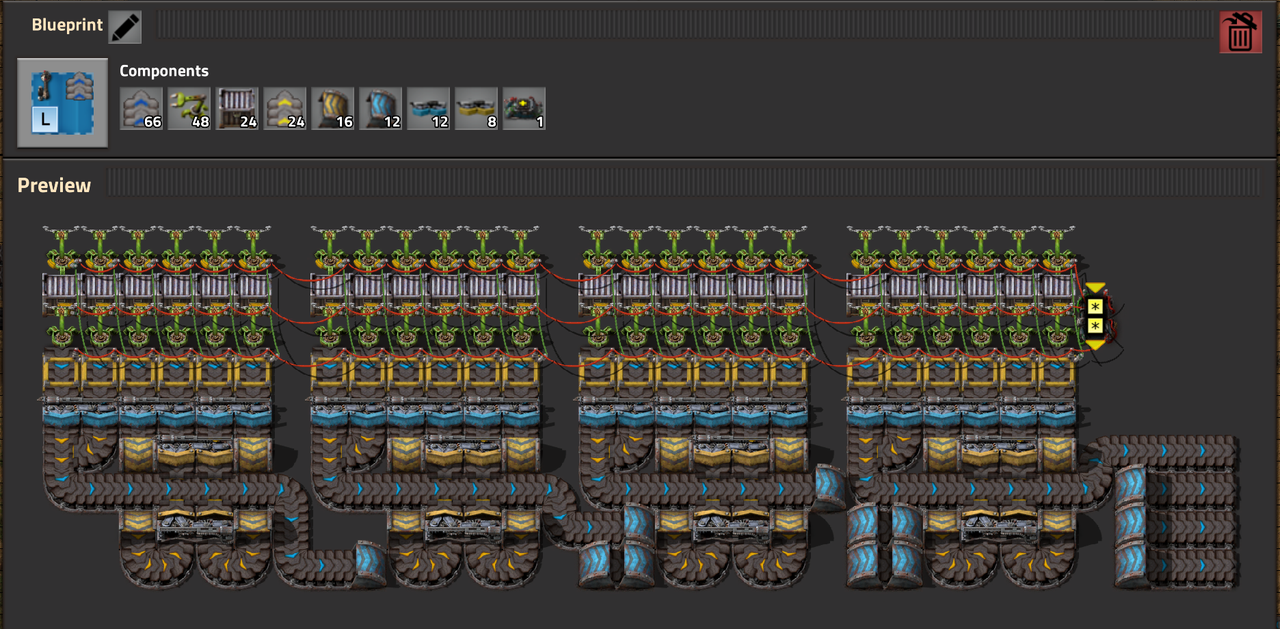
Image
This is my balanced train unloader. I wanted to create a solution that was fully balanced and this is the most compact thing I manage to create.
It uses madzuri logic circuits connection but provides full chest, lane balancing and belt balancing. (as long as you add a 4to4 or 8to8) while providing full throughput (2 compressed blue belts, one per side, per wagon)
Top
coppercoil
Filter Inserter
Filter Inserter
Posts: 502
Joined: Tue Jun 26, 2018 10:14 am
Contact:
Contact coppercoil

Re: my balanced train unloader

Post by coppercoil »

Are yellow splitters necessary?
Top
User avatar
disentius
Filter Inserter
Filter Inserter
Posts: 694
Joined: Fri May 12, 2017 3:17 pm
Contact:
Contact disentius

Re: my balanced train unloader

Post by disentius »

helps with balancing.
3x yellow -> 1x blue
Top
coppercoil
Filter Inserter
Filter Inserter
Posts: 502
Joined: Tue Jun 26, 2018 10:14 am
Contact:
Contact coppercoil

Re: my balanced train unloader

Post by coppercoil »

disentius wrote: ↑Wed Jun 12, 2019 10:20 pm helps with balancing.
3x yellow -> 1x blue
3x yellow are also splitted for two blue belt lanes, so single lane takes 1.5 of yellow. There should be no problems with the throughput.

Chest balancing is made by madzuri circuits, splitters are not necessary for this.
Top
User avatar
disentius
Filter Inserter
Filter Inserter
Posts: 694
Joined: Fri May 12, 2017 3:17 pm
Contact:
Contact disentius

Re: my balanced train unloader

Post by disentius »

4 cars, 8 blue belts, balanced, one sided.
Balanced unload 4 wagons 8 blue belts.gif
Balanced unload 4 wagons 8 blue belts.gif (5.48 MiB) Viewed 30394 times
Top
aberro
Burner Inserter
Burner Inserter
Posts: 13
Joined: Tue Mar 17, 2020 4:41 pm
Contact:
Contact aberro

Re: my balanced train unloader

Post by aberro »

If your lines are overloaded, then only two left-most crates per wagon will be unloaded, not all 6, because two left-most have priority so it's unbalanced.
Top
Post Reply

Return to “Railway Setups”